· Which of the following expressions are not equal to 1?As 1st equation is not true for $\theta$ equals to Stack Exchange Network Stack Exchange network consists of 176 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their · Which of the following is true for all values of θ (0° < θ < 90°) (a) cos2 θ – sin2 θ = 1 (b) cosec2 θ – sec2 θ = 1 (c) sec2 θ – tan2 θ = 1 (d) cot2 θ – tan2 θ = 1 Solution ∴ sec 2 θ – tan 2 θ = 1 is true for all values of θ as it is an identity (0° < θ < 90°) (c) Question 9

Prove That Tan 3 Theta 1 Tan 2theta Cot 3 Theta 1 Cot 2 Theta
2.tan^(2)theta(1)/(cot^(2)theta)-2 tan^(2)theta is equal to
2.tan^(2)theta(1)/(cot^(2)theta)-2 tan^(2)theta is equal to- · \cos ^{2} \theta=1\sin ^{2} \theta \\ \tan ^{2} \theta=\sec ^{2} \theta1 \\ \cot ^{2} \theta=\csc ^{2} \theta1 \end{array} \ Now that we have some basic identities to work with, let's use them to verify the equality of some more complicated statements The process of verifying trigonometric identities involves changing one side of the given expression into the other side · 2 tan 2 θ cot 2 θ sec θ cosec θ\frac {2 \tan^2 \theta \cot^2 \theta} {\sec \theta \cosec \theta} secθcosecθ2tan2θcot2θ is equal to So , the answer would be option c) sec θ cosec θ \sec\theta\cosec\theta s e c θ c o s e c θ Ask doubts feature is currently unavailable for you



Prove That 1 Tan Squared Theta Upon 1 Cot Squared Theta Is Equals To 1 Minus 10 Theta Upon 1 Minus Brainly In
If (3 π/4) < θ < π then √2 cot θ (1/ sin2 θ) is equal to (A) 1 cot θ (B) (1 cot θ) 1 cot θ (D) 1 cot θ Chec0911 · Defining Tangent, Cotangent, Secant and Cosecant from Sine and Cosine tan θ = sin θ cos θ cotFree math problem solver answers your algebra, geometry, trigonometry, calculus, and statistics homework questions with stepbystep explanations, just like a math tutor
Show that the identity 1\tan ^{2} \theta=\sec ^{2} \theta follows from \sin ^{2} \theta\cos ^{2} \theta=1 Join our free STEM summer bootcamps taught by experts Space is limitedRegister Here 🏕 Books;1401 · cot(theta) = 1/ tan(theta) = b / a Similarly, how do you solve CSC Theta?1 tan 2 θ = 1 ( e i θ − e − i θ i ( e i θ e − i θ)) 2 = 1 − ( e i θ − e − i θ) 2 ( e i θ e − i θ) 2 = ( e i θ e − i θ) 2 − ( e i θ − e − i θ) 2 ( e i θ e − i θ) 2 = e 2 i θ 2 e − 2 i θ − e 2 i θ 2 − e − 2 i θ ( e i θ e − i θ) 2 = 4 ( e i θ e − i θ) 2 = ( 2 e i θ e − i θ) 2 = sec 2 θ
· 1) Find an expression equivalent to sec theta sin theta cot theta csc theta tan theta csc theta sec theta ~ sin theta 2) Find an expression equivalent to cos theta/sin theta tan theta cot theta ~ sec theta csc theta 3) math;) Julia wants to simplify the term sec^2 theta1/cot^2 theta1 in a trigonometric identity that she is provingSolve your math problems using our free math solver with stepbystep solutions Our math solver supports basic math, prealgebra, algebra, trigonometry, calculus and moreCot (x) = cot (x) sin ^2 (x) cos ^2 (x) = 1 tan ^2 (x) 1 = sec ^2 (x) cot ^2 (x) 1 = csc ^2 (x) sin (x y) = sin x cos y cos x sin y cos (x y) = cos x cosy sin x sin y tan (x y) = (tan x tan y) / (1 tan x tan y) sin (2x) = 2 sin x cos x cos (2x) = cos ^2 (x) sin ^2 (x) = 2 cos ^2 (x) 1 = 1 2 sin ^2 (x)


How Do You Simplify Sin Theta Csc Theta Cot Theta Socratic


Prove That Cos Theta 1 Tan Theta Sin Theta 1 Cot Theta Cos Theta Sin Theta Youtube
θ = csc 2 θ − 1 The square of cot function equals to the subtraction of one from the square of cosecant function is called the cot squared formula It isProve the Following Trigonometric Identities (1 Tan^2 Theta)/(1 Cot^2 Theta) = ((1 Tan Theta)/(1 Cot Theta))^2 = Tan^2 Theta CBSE CBSE (English Medium) Class 10 Question Papers 6 Textbook Solutions Important Solutions 3111 Question Bank Solutions 334 Concept Notes & Videos & Videos 224 Time Tables 12 Syllabus Advertisement Remove all ads Prove · \(\frac { { 1tan }^{ 2 }A }{ { 1cot }^{ 2 }A } \) is equal to (a) sec 2 A (b) 1 (c) cot 2 A (d) tan 2 A Solution Question 7 If sec θ – tan θ = k, then the value of sec θ tan θ is (a) \(1\frac { 1 }{ k } \) (b) 1 – k (c) 1 k (d) \(\\ \frac { 1 }{ k } \) Solution Question 8 Which of the following is true for all values of θ



Prove Each Of The Following Identities Tan Theta 1 Cot Theta Cot Theta 1 Tan Theta Youtube


Solved 1 Tan Theta Tan Theta 1 Cos 2 Theta 1 Tan 2 Chegg Com
{eq}\cos 2\theta= \frac{\cot^2\theta 1}{1 \cot^2\theta} {/eq} Proving Trigonometric Identities A trigonometric identity is an equation in terms of trigonometric equations that is true for allGiven, tan 2 θ = 1 – e 2 sec θ tan 3 θ cosec θ = sec θ (sin 3 θ/cos 3 θ) (1/sin θ) = sec θ tan 2 θ sec θ = sec θ (1 tan 2 θ) = √ (1 tan 2 θ) (1 tan 2 θ) = (1 tan 2 θ) 3/2 = (1 1 – e 2) 3/2If sec theta = 1 1/4, then tan theta/2 is equal to


If Tan Theta Cot Theta 2 Then What Is The Value Of Tan Squared Theta Cot Squared Theta Equal To Quora
x-1=sec(squared)x.jpg)


10 Identity Tan Squared X 1 Sec Squared X Trigonometry Educator Com
· Beautiful blogs on basic concepts and formulas of mathematics, maths assignments for board classes, maths study material for 8th, 9th, 10th, 11th, 12th classes lesson plan for 10th and 12th, maths riddles and maths magic,2218 · (1 1/tan^2 theta)( 1 1/cot^2 theta) = 1/sin^2 theta sin^4 theta Get the answers you need, now!1cot2θ1tan2θ is equal to 1 cot 2 θ 1 tan



Prove That Tan 2 Theta Cot 2theta 2 Sec 2theta Cosec 2theta Brainly In



Prove That Cot Theta Tan Theta 2cos 2 Theta 1 Sintheta Cos Theta Brainly In
Well, cot theta is reciprocal of tan theta ie, cot theta = 1/tan theta If u didn't get it yet let me explain with an example suppose cot theta = 1/√3 than tan theta will be reciprocal of this ie, √3/1 that is √3 Also,product of cot and tan0318 · #1tan^2theta=sec^2 theta# #tan theta=sin theta/cos theta# and #sec theta=1/cos theta# #1sin^2theta/cos^2theta# = #1/cos^2theta# #cos^2thetasin^2theta # #/sin^2theta# = #1/cos^2theta# further on solving you would get both sides equal to sec^2 theta so it is provedLHS = `(sec^2 theta 1)(cosec^2 theta1)` =`tan^2 theta xx cot^2 theta ( ∵ sec^2 theta tan^2 theta = 1 and cosec^2 theta cot^2 theta =1)`



1 Tan 2theta Cot Theta Cosec 2 Theta Tan Theta Brainly In



Prove That 1 Cot Theta Cosec Theta 1 Tan Theta Sec Theta 2 Youtube
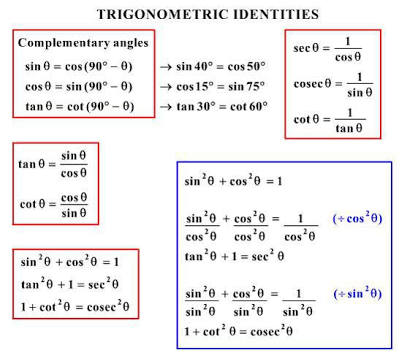
Take the inverse cosecant of both sides of the equation to extract θ from inside the cosecantIt can be written as1cot2A1tan2A = cosec2Asec2A = sin2A1 cos2A1 = cos2Asin2A = tan2ATherefore, Answer is tan2A0104 · $$\tan^{2}(\theta) 1 = \sec^{2}(\theta)$$ and $$\cot^{2}(\theta) 1 = \csc^{2}(\theta)$$ are trigonometric identities?????



Show That 1 Tan Squared Theta Cot Squared Theta 1 Tan Squared Theta Brainly In



If Theta 30 Verify That I Tan2theta 2tantheta 1 Tan 2theta Ii Sin2theta Youtube
Prove cot^2 theta (sec theta 1)/1sin theta = sec^2 theta(1sin Thema) /1sec theta Ask questions, doubts, problems and we will help you · prove that 1tan^2 theta/cot^2 theta1=tan^2 theta (theta not equal to 45 degrees) Math Introduction to Trigonometry$\tan^2 \theta 1 = \sec^2 \theta$ (okay!) $1 \left( \dfrac{\cos \theta}{\sin \theta} \right)^2 = \left( \dfrac{1}{\sin \theta} \right)^2$ $1 (\cot \theta)^2 = (\csc \theta)^2$ $1 \cot^2 \theta = \csc^2 \theta$ (okay!) s Trigonometry Pythagorean theorem identities Pythagorean identities Rate 0 No votes yet ‹ Derivation of Cosine Law up Derivation of Pythagorean Theorem



Prove That A Sin 2 Theta 1 Cos 2 Theta Tan Theta B 1 S


Solved Verify The Identities 1 1 Cos Theta 1 1 Cos Chegg Com
Trigonometric Identity sin^2 ( theta) cos^2 (theta) =1 Where theta is measure of an angle (typically between 0 to 2 pi radians but can have other values as well) From this identity, 1 cos^2 (theta) = sin^2 (theta) Answer 1 cos^2 (theta)= sin^2 (theta) Sanjay C 147K views ·Description for Correct answer cot 2 θ 1 cot 2 θ − 1 = 1 tan 2 θ 1 − tan 2 Pythagorean identities Main article Pythagorean trigonometric identity In trigonometry, the basic relationship between the sine and the cosine is given by the Pythagorean identity sin 2 θ cos 2 θ = 1 , {\displaystyle \sin ^ {2}\theta \cos ^ {2}\theta =1,}



Cot Theta Minus Tan Theta Is Equal To 2 Cos Squared Theta Minus 1 By Sin Theta Cos Theta Brainly In
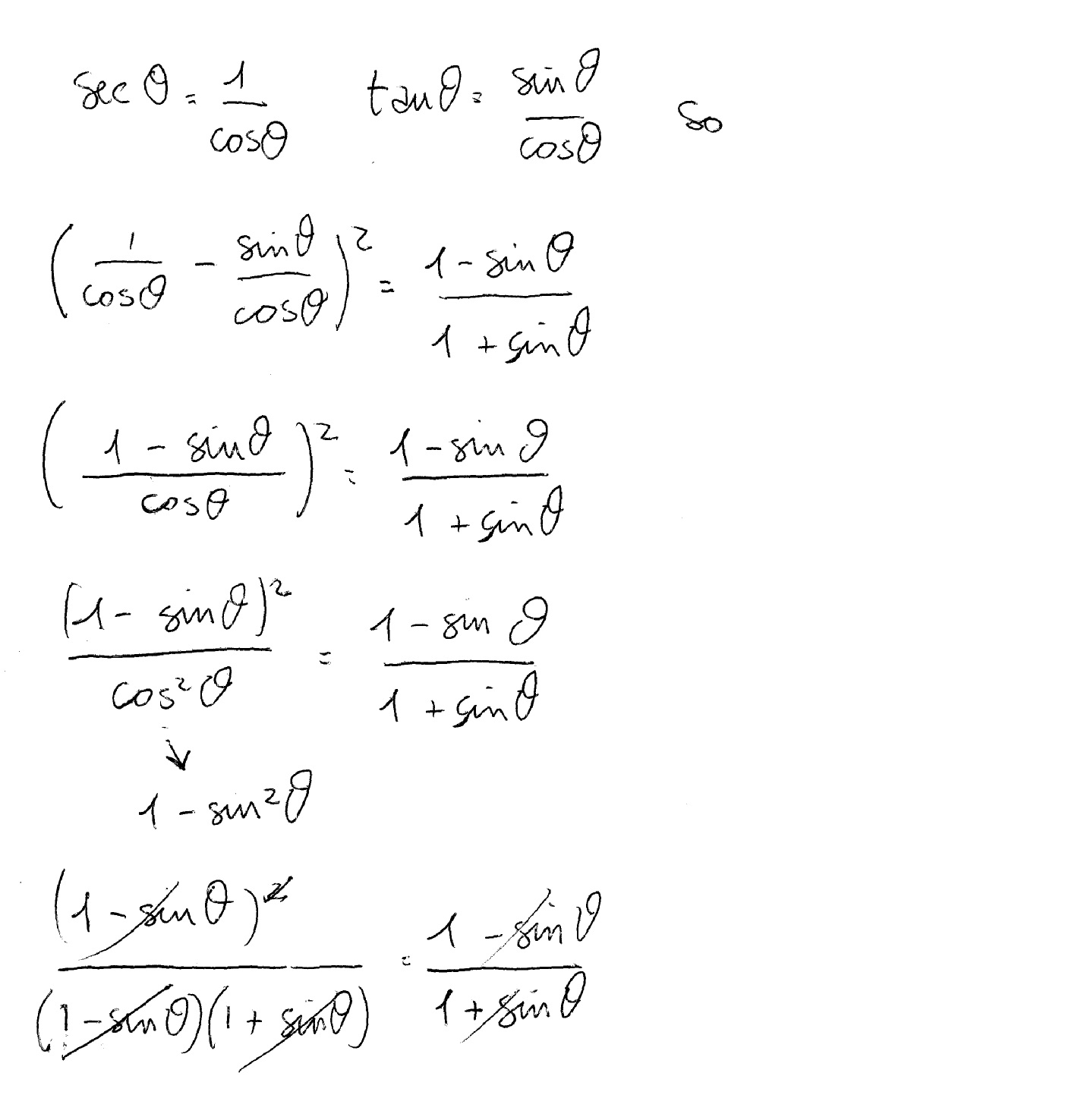


How Do You Prove The Identity Sectheta Tantheta 2 1 Sintheta 1 Sintheta Socratic
Free Question Bank for 10th Class Mathematics Introduction to Trigonometry Trigonometry · Prove that (1 1/ tan2theta) (1 1/cot2theta) = 1/sin2theta sin4theta Maths Introduction to TrigonometryThere is no answer available Request an answer



Solved Example Trigonometry Prove 1 Tan 2 A 1 Cot 2 A Sin 2 A Cos 2 A Youtube


If Tan 8 1 Tan 8 2 What Is The Values Of Tan 8 1 Tan 8 Quora
A) sin^2 theta cot^2 theta sin^2 theta B) (sin^2 theta/1cos theta)cos theta C) sec^2 theta tan^2 theta D) cot^2 theta sin^2 theta/cos^2theta Answer D Lucy Apr 19, 08 for D I get c^2/s^2 * s^2 /c^2 = 1 sorry A gives s^2 (1 c^2/s^2) = s^2 c^2 = 1 B gives (does not make sense the way you wrote it) Maybe you mean sin^2 theta/(1Join for Free Problem Show that the identity $$ 1\cot ^{2} \theta=\csc Uh oh!The value of \( \Large \left(\frac{1}{(1tan^{2} \theta )}\frac{1}{(1cot^{2} \theta )}\right) \) is



Prove That 1 Cosec 2alpha Tan2 Theta 1 Cosec 2beta Tan 2theta 1 Cot 2alpha Sin 2theta 1 Youtube



1 Tan 2x 1 Tan 2 X 1 2cos 2 X Youtube
· ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS ML Aggarwal Class 10 Solutions for ICSE Maths Chapter 18 Trigonometric Identities MCQS Choose the correct answer from the given four options (1 to 12) Question 1 is equal to (a) 1 (b) 1 (c) sin2 θ (d) sec2 θ SolutionVITEEE 10 The value of ( cosθ/1 sinθ) is equal to (A) tan((θ/2) (π/4)) (B) tan( (π/4) (θ/2) ) tan( (π/4) (θ/2) ) (D) tan


What Is The Answer Of Math Frac Tan Theta 1 Cot Theta Frac Cot Theta 1 Tan Theta Math Quora


Can You Prove That Math Frac 1 Tan 2 Theta Cot 2 Theta 1 Tan 2 Theta Math Quora



Solved 1 Tan Squared Theta Into 1 Cot Square Theta Is Equals To 1 By Sin Squared Theta Minus Sin Brainly In



Simplify 1 Tan 2 Theta 1 Sin Theta 1 Cos Theta Brainly In



14 1 Trigonometric Identities Ppt Download



If Tan Theta Sec Theta 2 Then What Is Tan Theta Is Equal To Quora



Prove That 1 Tan 28 1 Cot 28 1 Tan8 1 Cot8 2 Tan 28



Show That Tan3 Theta 1 Tan2 Theta Cot3 Theta 1 Cot2 Theta Sec Theta Cosec Theta 2sin Theta Cos Theta Maths Introduction To Trigonometry Meritnation Com



Let F N Theta Tan Theta 2 1 Sec Theta 1 Sec 2theta 1 Sec 2 Ntheta Then Youtube



Cot Theta Tan Theta 2cos Square Theta 1 Upon Sin Theta Cos Theta Brainly In



Prove That 1 1 Tan 2 Theta 1 1 Cot 2 Theta 1



Solve Sin 2 Theta Tan Theta Cos 2 Theta Cot Theta Sin 2 Theta 1 T
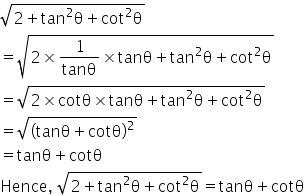


Prove That 2 Tan2 Cot2 Tan Cot Mathematics Topperlearning Com Ttevdk55



What Is The Value Of Sin 2theta 1 1 Tan 2theta



1 1 Tan 2 Theta 1 1 Cot 2 Theta 1 Sin 2 Theta Sin 4 Theta Brainly In



1 Tan 2theta 1 Cot 2theta 1 Tan Theta 1 Cot Theta 2 Tan 2 Theta Brainly In



Prove That Tan Theta 1 Cot Theta Cot Theta 1 Tan Theta 1 Sec Theta Cosectheta Brainly In



Prove That 1 1 Tan 2 Theta 1 1 Cot 2 Theta 1



Cos 2 Theta 1 Tan Theta Sin 3 Theta Sin Theta Cos Theta 1 Sin Theta Cos Theta Brainly In



The Numerical Value Of 1 1 Cot 2 Theta 3 1 Tan 2 Theta 2



Prove That 1 Tan Squared Theta Upon 1 Cot Squared Theta Is Equals To 1 Minus 10 Theta Upon 1 Minus Brainly In



1 Cot Theta Cosec Theta 1 Tan Theta Sec Theta 2 Youtube



If Tan Theta Cot 2 Theta Then The Value Of Theta Is Youtube



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



Prove That Cot Theta Tan Theta 2 Cos 2 Theta 1 Sin Theta Cos Theta Youtube



The Expression Tan 4 Theta Tan 2 Theta Left 1 Tan 2 3 Theta Tan 2 Theta Right Is



Sec 2 Theta 1 Tan 2 Theta Youtube


Solving Trigonometric Equations With Identities Precalculus Ii



Verify That Csc 2 Theta Cot 2 Theta 1 Youtube



Prove That A Sin 2 Theta 1 Cos 2 Theta Tan Theta B 1 Sin 2 Theta 2theta Youtube



Tan Theta 1 Tan 2 Theta 2 Cot Theta 1 Cot 2 Theta 2 Sin Theta Cos Theta Brainly In



How Do You Verify The Identity Csctheta Cottheta Csctheta Cottheta 1 Socratic



1 Tan Square Theta 1 Cot Square Theta 1 Tan Theta 1 Cot Theta Whole Square Tan Square Theta Brainly In



Prove That 1 Tan 2 Theta Cot 2 Theta 1 Tan 2 Theta



What Is The Value Of 1 Cot Theta Cosec Theta 1 Tan Theta Sec Theta Quora
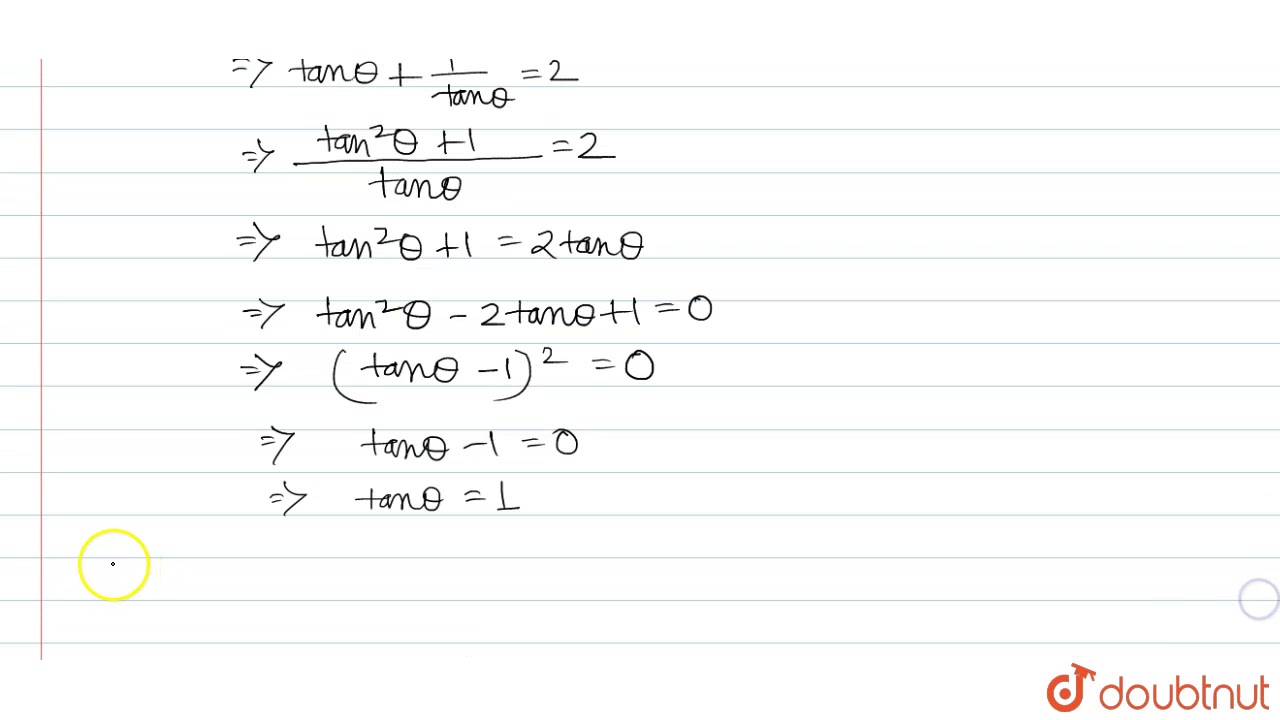


If Tan Theta Cot Theta 2 Then Dtemine The Value Of Tan Theta Cot Theta Youtube



5 1 Fundamental Trig Identities Sin 1cos 1tan 1 Csc Sec Cot Csc 1sec 1cot 1 Sin Cos Ppt Download


Prove That Math Tan 2 Theta 1 Sec 2 Theta Math Quora



1 1 Tan Theta 1 Cot Theta 2 Sec 2 Mathematics Topperlearning Com Ggw6mtpp



If Tan 2 Theta 1 2 Tan 2 Phi Prove That Cos 2 Phi 1 2 Cos 2
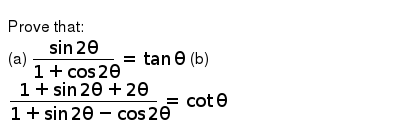


Prove That A Sin 2 Theta 1 Cos 2 Theta Tan Theta B 1 S


How Do You Verify Tan 28 Sin 28 Tan 28sin 28 Socratic



Solved Establish The Identity 1 Tan 2 Theta 1 Tan 2 Chegg Com



Prove That 1 Tan Theta Upon 1 Cot Theta 1 Tan Theta Upon 1 Cot Theta Brainly In



Trigonometric Identities List Of Trigonometric Identities Examples



Prove 1 Cot 2 Theta Csc 2 Theta Mathematics Stack Exchange



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



Why Is Math Csc 2 Theta Cot 2 Theta 1 Math Quora


Prove That 1 Tan 2 8 1 Cot 2 8 1 Tan 8 Cot 8 2 Tan 2 8 Sarthaks Econnect Largest Online Education Community


Prove That Math Tan 2 Theta 1 Sec 2 Theta Math Quora



If Tan Theta 1 2 Then Find The Value Of 2 Cot Square Theta 2 Brainly In



Prove That Tan 3 Theta 1 Tan 2theta Cot 3 Theta 1 Cot 2 Theta
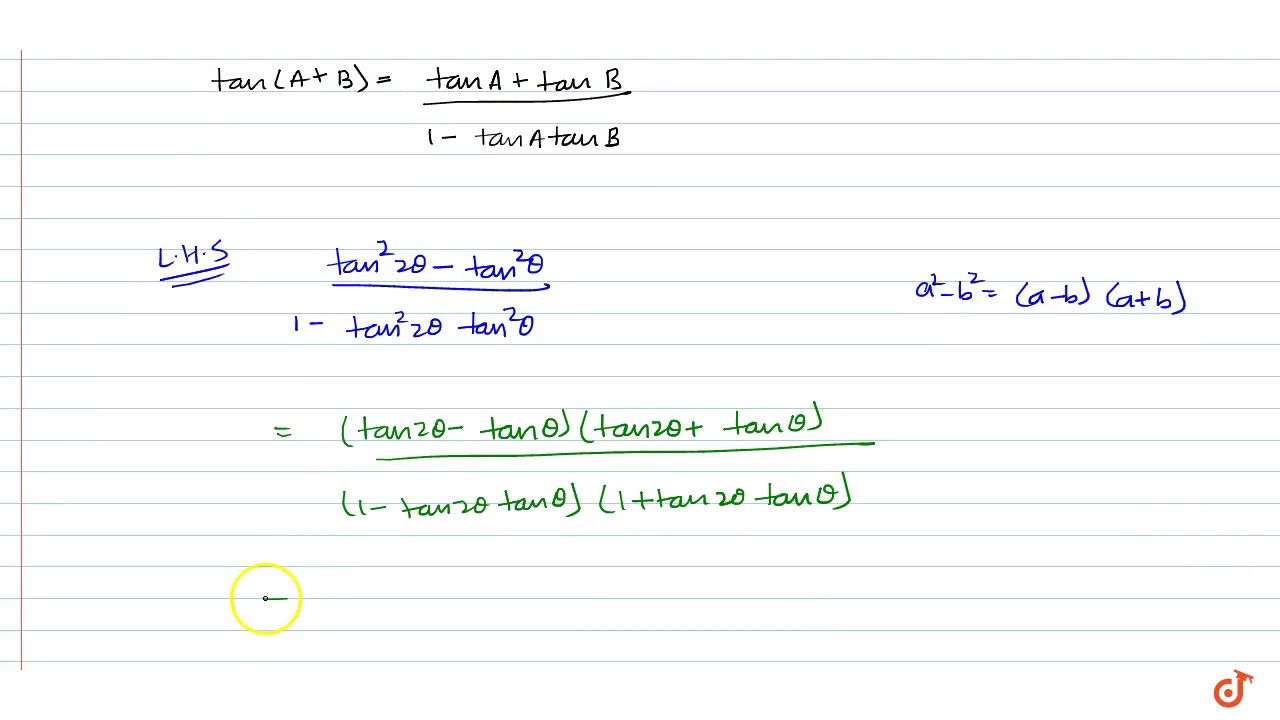


Prove That Tan 2 2theta Tan 2 Theta 1 Tan 2 2theta Tan 2 Theta Tan 3theta Tan Theta Youtube



Tan 2 Theta Sec Theta 1 2 1 Cos Theta 1 Cos Theta Youtube


How To Solve The Equation 2 Tan Theta Cot Theta 1 Quora



How Does One Prove That Math Sec 2 Theta Tan 2 Theta Csc 2 Theta Cot 2 Theta 1 2 Sec 2 Theta Csc 2 Theta Text Math Quora



Show That 1 1 Tan Square Theta 1 1 Cot Square Theta 1 Sin Square Theta Sin 4 Theta Maths Introduction To Trigonometry Meritnation Com



If Tan 2 Theta 1 2 Tan 2 Phi Prove That Cos 2 Phi 1 2 Cos 2 Theta Youtube


If Cot 8 15 8 Then How Do You Find The Value Of 2 2sin8 1 Sin8 1 Cos8 2 2cos8 Quora


How Do You Prove 1 Sin 2theta 1 Cot 2theta Cot 2theta Socratic



Tan Theta 1 Cot Theta Cot Theta Divided By 1 Minus 10 Theta Equal To 1 Secant Theta Into Cos Youtube


Prove That Tan 8 1 Cot 8 Cot 8 1 Tan 8 1 Tan8 Cot 8 Studyrankersonline



Prove That Tan 2 Theta 1 Tan 2 Theta Cot 2 Theta 1



Prove That 1 Tan Theta Tan 2theta Sec 2theta Youtube


Proof Of The Identity 1 Cot 2 Theta Cosec 2 Theta Proved Cot 2 X 1 Cosec 2 X Youtube



Tangent Half Angle Formula Wikipedia



Prove That Cot 8 Tan 8 2 Cos 2 8 1 Sin 8 Cos 8
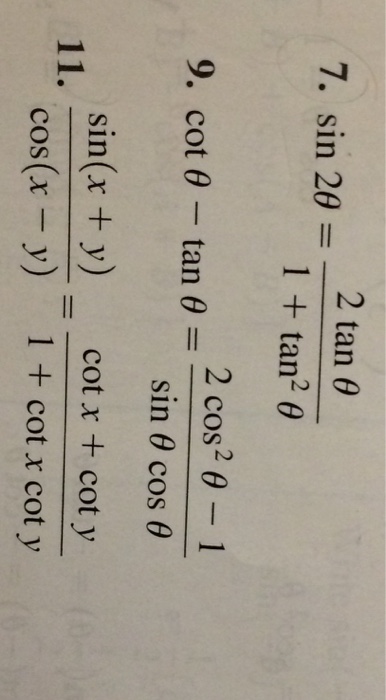


Solved Sin 2 Theta 2 Tan Theta 1 Tan 2 Theta Cot Thet Chegg Com



Prove Tan 2 Theta Cot 2 Theta Cosec 2 Theta Sec 2 Theta Brainly In



Prove That 1 Tan 2 Theta 1 Cot 2 Theta 1 Tan Theta 1 Cot Theta 2 Brainly In
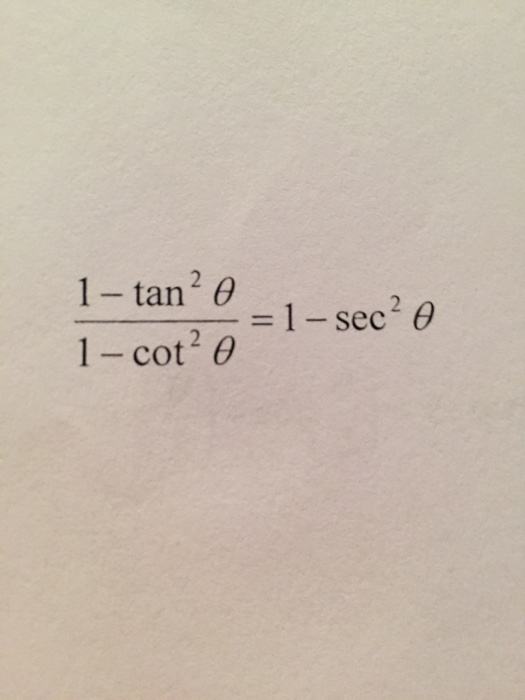


Solved 1 Tan 2 Theta 1 Cot 2theta 1 Sec 2theta Ve Chegg Com



Trigonometric Identities Ppt Download


What Is The Value Of 1 Cot Theta Cosec Theta 1 Tan Theta Sec Theta Quora


How Would One Prove That 1 Tan Theta Sec Theta 1 Cot Theta Cosec Theta 2 Quora



Prove That Tan 2 2theta Tan 2 Theta 1 Tan 2 2theta Tan 2 Th


What Is The Value Of 1 Cot Theta Cosec Theta 1 Tan Theta Sec Theta Quora
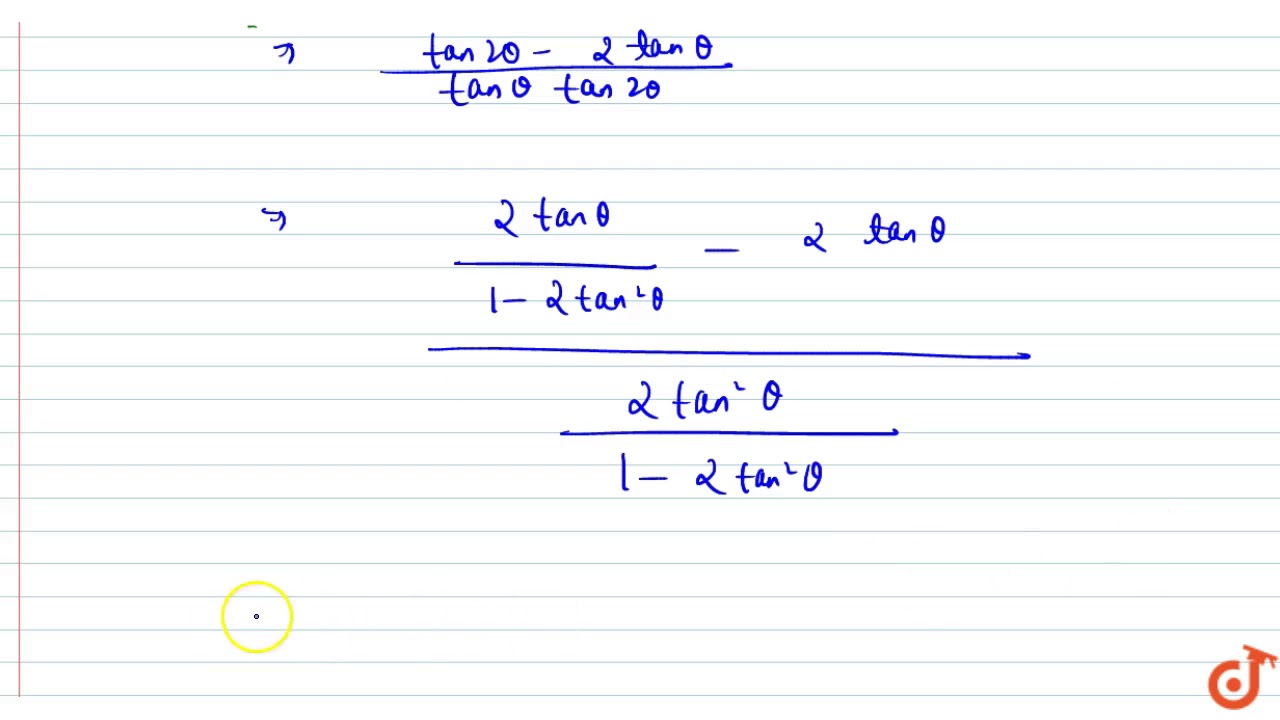


For All Real Values Of Theta Cot Theta 2 Cot 2theta Is Equal To Youtube



Prove That Cot Theta 1 Tan Theta Cot Theta 1 2 Sec 2 Theta Brainly In



Rd Sharma Solutions For Class 10 Chapter 6 Trigonometric Identities Exercise 6 1 Get Pdf



Theta Tan 1 2 Tan 2 Theta Tan 1 1 3 Tan Theta


